646 Videos

Videos for Economics of Derivatives

The bulk of videos for this course are actually voice-over slides covering material in the Coursepack. You can link to these videos from the course Blackboard site. There are a number of videos and films to which you can link from this page that might be helpful to you in this course. Some of these are made by professionals, some by amateurs and even a few starring myself. But, sadly, high-end popular educational films in finance, especially derivatives, that gets film buffs all abuzz really aren't particularly common.

Remedial Videos on Black Scholes

Some students in this course are likely not to have seen the Black-Scholes model in prior classes. Here are two videos that I made with Gianpiero Alicchio and Allegra Sappio of LUISS that introduce just the non-technical basics of these topics. So, if you read about these topics in the Coursepack and are having problems, start be having a look at these videos. Bear in mind that I am based in New York, while Gianpiero and Allegra are in Rome, so there are still a few minor glitches in the videos. Partly because of these glitches, I recommend that you see the notes below before or while you view the videos.

John Teall - The Black-Scholes Options Pricing Model

https://vimeo.com/351000132/6a9d6fa53a

This video introduces the important Black-Scholes Options Pricing Model to the valuation of simple "plain vanilla" stock options, calls and puts.
The following are notes that might be helpful to you when viewing the video. I recommend pausing the video during the times listed in the far left to pay attention to the notes towards the center and right:
Time	S₀ = 75		X = 80	T = .5	s² = .16	r_f = .10	s = .4	c₀ = ?
	Underlying		Exercise	Expiration	Underlying	Riskless	Underlying	Call
1:24-1:27	Price		Price	Date	Return	Return	Standard	Price
					Variance	Rate	Deviation
2:16-22		The Black-Scholes Model is in the box on the right. We will fill in the values from the left of the video into the box.
2:22-33		Starting with the equation for d₁, we fill in values, finding that d₁ = 0.09. Then, we fill in values for d₂, finding that d₂ = -0.1928 (the equals sign before it is missing).
2:43-2:53		Next, we get the N(d₁) and N(d2) values from a z-table. Since different z-tables handle areas to the left of the mean differently, under the normal curve the value .5 might or might not be added or subtracted from the value at the appropriate intersection of row and column. But, each table will be consistent from example to example.
2:58-3:06		Now, insert the N(d₁) and N(d2) into the c₀ equation to complete the calculation.
3:19-3:47		Don't stop the video. Instead, look at the following equation: Also, I made a mistake at time = 3:26, saying "minus" when I should have said "plus."

John Teall - Implied Volatility
https://vimeo.com/351001396/65adcc8764

This video applies the Black-Scholes Option Pricing Model to the calculation of underlying stock (or asset) variances based on option (or equity) market prices.

The following are notes that might be helpful to you when viewing the video. I recommend pausing the video during the times listed in the left to pay attention to the notes towards the center and right:

2:49-3:17

T = .5

r = .10

c₀ = 7.00

X = 80

S₀ = 75

If investors use the Black-Scholes Options Pricing Model to value calls, the following should be expected:

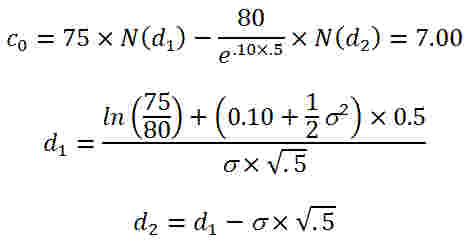
Black-Scholes Model

3:21-3:32

Just compare what is written above to what is on the screen. Notice that the calculated call price c₀ = 7.958 > 7.00 is too high. We will need to try again with a lower standard deviation estimate.

Instructional Videos that Correspond to our Derivatives Sessions
Running a course online through Zoom or Blackboard can be dreadful for a number of reasons. Students often find reading long dense pdf files about banking to be even more dreadful. In an effort to make some part of this material more palatable to students, I propose that you consider watching a few fairly well-made films for some comic relief. It is not essential that students view any of the following videos if they are able to read and fully comprehend the Coursepack. The videos just might be more enjoyable for some students and may make it easier to fully understand the material in the Coursepack for some. Unfortunately, the videos will certainly not cover all of the material required for exam purposes. Some of the videos below are well-made and entertaining, which might help students stick with their efforts a little longer. In case problems arise due to your url, firewalls and the like, multiple links are provided for most videos.

Trillion Dollar Bet (2000): This documentary tells a story of the Black-Scholes-Merton options pricing formula and the collapse of hedge fund Long-Term Capital Management (LTCM). It includes interviews with Robert Merton and Myron Scholes, who won the Nobel Prize in Economics in 1997. Some of the stories involving academics are true, some are a little misleading. Some are dead-on right, such as the story told by Paul Samuelson concerning Louis Bachelier and the discussion of Itô Calculus. The "dark side" stories of the narrator seem to reflect a lack of knowledge trading and financial modeling, but no real harm done, but many of the descriptions of basic options are pretty good. The video omits discussion well-known and visually similar formulas that existed at the time developed by Sprenkle and Samuelson. The key insight of the Black-Scholes-Merton formulations is the dynamic hedge ratio, as discussed in the film. There are striking similarities between the failure of resolution of LTCM and the Financial Crisis of 2008. One insightful quote at the end, by Paul Samuelson, citing Albert Einstein: "Elegance is for tailors." This would be a wonderful film for the right finance course. Available for free, as of April 2020 at https://watchdocumentaries.com/trillion-dollar-bet/, https://docur.co/documentary/trillion-dollar-bet, https://archive.org/details/TrillionDollarBet and https://vimeo.com/244903345.

Panic: The Untold Story of the 2008 Financial Crisis: Full VICE Special Report: Excellent HBO documentary detailing the events leading up to the failure of Lehman Brothers. Available on HBO-Go and, as of April 2020, available on Youtube at https://www.youtube.com/watch?v=QozGSS7QY_U, https://topdocumentaryfilms.com/panic-untold-story-2008-financial-crisis/, https://www.youtube.com/watch?v=wyz79sd_SDA, and https://www.forbes.com/sites/rogervaldez/2019/05/26/must-watch-the-untold-story-of-the-2008-financial-crisis/#6db2da982352. Most of these web pages have a connection to Youtube.

Films and Videos that Might be a Little Bit Instructional in a Derivatives Course, but Likely to be More Entertaining
While many of the films on this list were popular, their educational value might questionable, or at least aren't quite relevant to our course. Nevertheless, they might be more entertaining than the Coursepack. I have not looked at films closer to the bottom of the list. All of these films are available online somewhere, but many will probably require some sort of subscription to view. Links to free sites are provided where available.

Trading Places (1983): A rather silly comedy starring Eddie Murphy that actually stands out among popular films concerning finance and financial trading. While, for the most part, the film is downright silly, it does include some dramatic and even somewhat realistic depictions of a number of important concepts crucial to traders. There were real parallels between actual trading and the trading action in the film. It might be worth looking online to list how others have listed some of the parallels between the film and actual trading floors. Some observers have suggested that the film was inspired by a real-life social experiment of trading partners William Eckhardt and Richard Dennis, who sought to learn whether successful trading could be taught.

The Ascent of Money (2008) In this 6-part documentary, based on a book with the same title, Niall Ferguson, author and academic, traces the evolution of money, bond markets, insurance, bubbles, the subprime mortgage debacle, etc. A key lesson from this video is the same as what historians regularly remind us: This time is not so different; it has happened before — and more than once. Has applications to Sessions 2 and 7. At least three of the 6 parts are available through PBS online at https://www.pbs.org/video/the-ascent-of-money-part-1-from-bullion-to-bubbles/, https://www.pbs.org/video/the-ascent-of-money-part-2-bonds-of-war/, and https://www.pbs.org/video/the-ascent-of-money-part-3-risky-business/. It appears that all 6 segments are available at https://www.youtube.com/watch?v=fsrtB5lp60s.

Floored (2009): A documentary by the trader James Allen Smith is instructional and might be of interest to students, but doesn't really intersect with material covered in our particular course. This documentary concerns the decline of the Chicago Trading Pits and traders' responses and efforts to adapt to electronic trading.

Growth of the Finance Industry (2019): Narrated by Philip Short, this 8-part series of 12-minute segments chronicles the past 100 years of the development of Shanghai's banking and financial industries. Free with Amazon Prime, and approximately $6 for all 8 parts through Amazon (paid; free with Amazon Prime) at https://www.amazon.com/Growth-Finance-Industry/dp/B07HFJHS6Z.

Inside Job (2010): Documentary concerning the Financial Crisis of 2008.

Rogue Trader (1999): Acted film based on Nick Leeson and Barings Bank.

The Big Short (2015) In 2006-2007 a group of investors bet against the US mortgage market. In their research they discover how flawed and corrupt the market is.

The Flaw (2011) 78 minute analysis of the financial crisis


646	HOME

Updated 01/23/2021